Suma o adición
Dadas las matrices m-por-n A y B, su suma A + B es la matriz m-por-n calculada sumando los elementos correspondientes (i.e. (A + B)[i, j] = A[i, j] + B[i, j] ). Es decir, sumar cada uno de los elementos homólogos de las matrices a sumar. Por ejemplo:
Propiedades
- Asociativa
Dadas las matrices m×n A, B y C
- A + (B + C) = (A + B) + C
- Conmutativa
Dadas las matrices m×n A y B
- A + B = B + A
- Existencia de matriz cero o matriz nula
- A + 0 = 0 + A = A
- Existencia de matriz opuesta
con -A = [-aij]
- A + (-A) = 0
Producto
El producto de dos matrices se puede definir sólo si el número de columnas de la matriz izquierda es el mismo que el número de filas de la matriz derecha. Si A es una matriz m×n y B es una matrizn×p, entonces su producto matricial AB es la matriz m×p (m filas, p columnas) dada por:
para cada par i y j.
Por ejemplo:
Propiedades
Si los elementos de la matriz pertenecen a un cuerpo, y puede definirse el producto, el producto de matrices tiene las siguientes propiedades:
- Propiedad asociativa: (AB)C = A(BC).
- Propiedad distributiva por la derecha: (A + B)C = AC + BC.
- Propiedad distributiva por la izquierda: C(A + B) = CA + CB.
- En general, el producto de matrices tiene divisores de cero: Si A.B = 0 , No necesariamente A ó B son matrices nulas
- El producto de matrices no verifica la propiedad de simplificación: Si A.B = A.C, No necesariamente B=C
El producto de dos matrices generalmente no es conmutativo, es decir, AB ≠ BA. La división entre matrices, es decir, la operación que podría producir el cociente A / B, no se encuentra definida. Sin embargo, existe el concepto de matriz inversa, sólo aplicable a lasmatrices cuadradas.
Producto por un escalar
Dada una matriz A y un escalar c, su producto cA se calcula multiplicando el escalar por cada elemento de A (i.e. (cA)[i, j] = cA[i, j] ).
Ejemplo
Propiedades
Sean A y B matrices y c y d escalares.
- Clausura: Si A es matriz y c es escalar, entonces cA es matriz.
- Asociatividad: (cd)A = c(dA)
- Elemento Neutro: 1·A = A
- Distributividad:
- De escalar: c(A+B) = cA+cB
- De matriz: (c+d)A = cA+dA
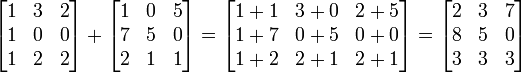
![(AB)[i,j] = A[i,1] B[1,j] + A[i,2] B[2,j] + ... + A[i,n] B[n,j] \!\](http://upload.wikimedia.org/math/3/6/8/3685038eaea4a600957beea930ad474c.png)

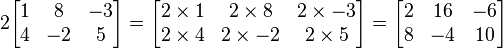


No hay comentarios:
Publicar un comentario